Animatable Neural Radiance Field for Modeling Dynamic Human Bodies
Published:
Animatable NeRF is the latest outcome of ZJU 3D Vision Lab. Animatable NeRF reconstructs an animatable human model from a multi-view video. They introduce neural blend weight fields to produce the deformation fields. Based on the skeleton-driven deformation, blend weight fields are used with 3D human skeletons to generate observation-to-canonical and canonical-to-observation correspondences.

输入一段稀疏多视角的视频,论文希望生成一个可驱动的人体模型,即输入新的人体姿态,可以生成相应姿态下的人体图片,而且可以生成自由视点下的图片。
论文提出神经混合权重场(neural blend weight field)以产生形变场(deformation field)表示人体动作的表示方法,通过人体骨骼驱动产生观察帧和正则帧的形变对应关系,结合nerf恢复可驱动的人体模型。此外,改变人体关键点位置也可以和学得的混合权重场产生新的形变场来驱动人体模型。
这种方法有两个优点:1. 人体骨骼方便捕捉,网络容易规范regularization;2. 通过正则空间学习一个额外的混合权重场,我们能够利用现有的nerf场合成新动作。
该问题有很多应用,比如自由视角观赛、虚拟视频会议、影视制作。
方法
对于每一帧,首先获取人体的 3D 人体骨骼,背景部分的像素值全部设为0。
论文将视频表示为一个正则人体模型(由 NeRF 表示)和逐帧的变形场,其中变形场用线性蒙皮模型(LBS)表示。具体步骤为:
- 给定一个视频帧空间的三维点,论文在视频帧坐标系定义了一个neural blend weight field,使用全连接网络将三维点映射为蒙皮权重。
- 输入当前视频帧下的人体骨架,生成变换矩阵,使用线性蒙皮模型将三维点转回标准坐标系。
- 论文在标准坐标系上定义了一个 NeRF 场。对于变换后的点,我们用 NeRF 场预测三维点的 volume density 和 color。

1 将视频表示为 NeRF 场 Representing videos with nerf
对于视频的每一帧 $i \in { 1, …, N}$ 都定义一个定义形变场 $T_i$,把视频帧的点转换到正则空间中。下面定义正则空间中的NeRF模型,分为密度模型和颜色模型。
正则空间中的密度模型 Density Model
\[\begin {equation} \left(\sigma_{i}(\mathbf{x}), \mathbf{z}_{i}(\mathbf{x})\right)=F_{\sigma}\left(\gamma_{\mathbf{x}}\left(T_{i}(\mathbf{x})\right)\right) \end {equation}\]$\mathbf{z}{i}$ 是原来 nerf 中的形状特征,$\gamma{\mathbf{x}}$ 代表坐标的位置编码 positional encoding
正则空间中的颜色模型 Color Model
每帧定义latent code: ${\ell}_{i}$
\[\begin {equation} \mathbf{c}_{i}(\mathbf{x})=F_{\mathbf{c}}\left(\mathbf{z}_{i}(\mathbf{x}), \gamma_{\mathbf{d}}(\mathbf{d}), \boldsymbol{\ell}_{i}\right) \end {equation}\]$\gamma_{\mathbf{d}}$ 是观察方向的位置编码
2 形变场/神经混合权重场 Neural blend weight field
2.1 线性蒙皮模型 Linear Blend Skinning Model
正则空间中的点 $\mathbf v$ 通过如下关系映射到视频帧:
\[\begin {equation} \mathbf{v}^{\prime}=\left(\sum_{k=1}^{K} w(\mathbf{v})_{k} G_{k}\right) \mathbf{v} \end {equation}\]人体骨骼定义 $K$$w(\mathbf{v}){k}$是第 每个部分对应一个变换矩阵 ${G_k } \in SE(3)$。$w(\mathbf{v}){k}$表示第 $k$ 个部分的混合权重。
类似的,对于一个视频帧中的点,根据该帧定义的混合权重 $w^{o}(\mathbf{x})$,我们可以把它变换到正则空间中
\[\begin {equation} \mathbf{x}^{\prime}=\left(\sum_{k=1}^{K} w^{o}(\mathbf{x})_{k} G_{k}\right)^{-1} \mathbf{x} \end {equation}\]
2.2 蒙皮权重的求解 Obtaining blend weight per frame
如果让网络直接输出蒙皮权重,会容易收敛到局部最小值。为了解决这个问题,我们首先对任意三维点赋予一个初始化的SMPL蒙皮权重,然后用 MLP 网络 $F_{\Delta \mathbf{w}}:\left(\mathbf{x}, \boldsymbol{\psi}{i}\right) \rightarrow \Delta \mathbf{w}{i}$ 预测一个残差值 residual vector($\psi_{i}$ 是每帧通过学习得到的latent code,$\Delta \mathbf{w}_{i}\in \mathbb{R}^{K}$是残差向量),两者相加得到最终的蒙皮权重。
第 $i$ 帧的蒙皮权重场定义为:
\[\begin {equation} \mathbf{w}_{i}(\mathbf{x})=\operatorname{norm}\left(F_{\Delta \mathbf{w}}\left(\mathbf{x}, \boldsymbol{\psi}_{i}\right)+\mathbf{w}^{\mathrm{s}}\left(\mathbf{x}, S_{i}\right)\right) \end {equation}\]${w}^{\mathrm{s}}$ 是基于SMPL模型 $S_i$ 计算出的初始权重,对任意的3D点,首先找到SMPL mesh 表面最近的点,然后在相应的mesh facet上的三个vertex的蒙皮权重使用 barycentric interpolation 计算出对应的 blend weight。$\operatorname{norm}(\mathbf{w})=\mathbf{w} / \sum w_{i}$。

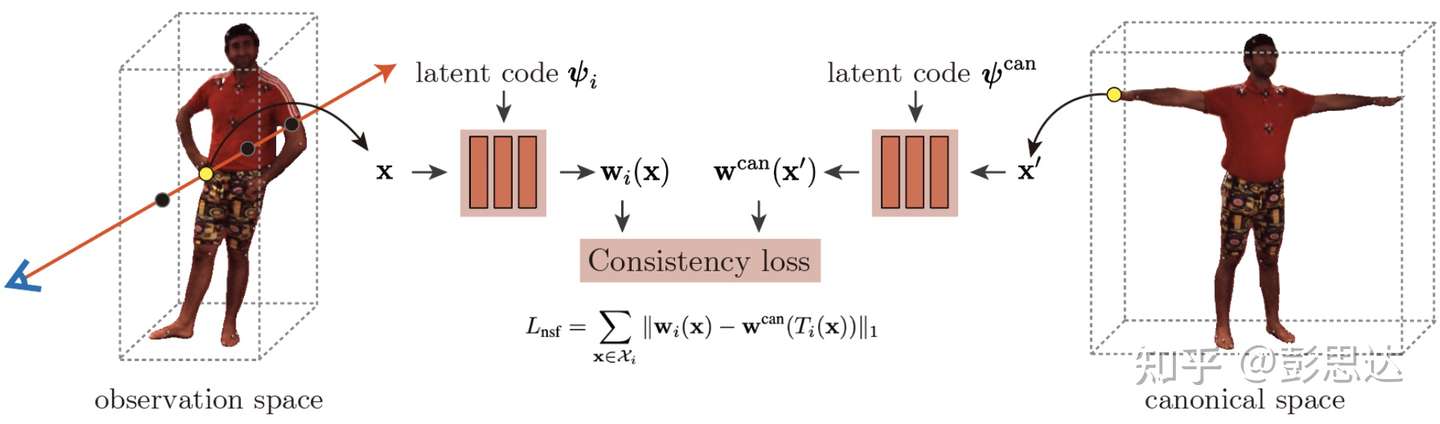
2.3 正则空间的蒙皮权重场 $\mathbf w ^\text{can}$
为了驱动习得的模版 NeRF 场,还需要额外学习正则空间的neural blend weight蒙皮权重场 $\mathbf w ^\text{can}$。这时,SMPL蒙皮权重 $\mathbf w^\text{can}$根据 T-pose SMPL静止状态计算得出,$F_{\Delta \mathbf{w}}$ 需要根据额外的 latent code $\psi ^\text{can}$ 计算。论文通过约束让视频帧坐标系和正则坐标系的对应点的blend weight相同来学习正则空间中的 neural blend weight field。
3 训练
$F_{\sigma}, F_{\mathbf{c}}, F_{\Delta \mathbf{w}},\left{\boldsymbol{\ell}{i}\right}, \left{\boldsymbol{\psi}{i}\right}$通过最小化渲染和gt误差优化:
\[\begin {equation} L_{\mathrm{rgb}}=\sum_{r \in \mathcal{R}}\left\|\tilde{\mathbf{C}}_{i}(\mathbf{r})-\mathbf{C}_{i}(\mathbf{r})\right\|_{2} \end {equation}\]$\mathcal{R}$ 是通过图片像素点的光线集合。
在驱动人体模型时,我们需要优化视频帧坐标系下的neural blend weight field。这个也是通过约束视频帧坐标系和正则坐标系的对应点的blend weight相同来进行训练。需要注意的是,正则坐标系的neural blend weight field在训练新动作的人体模型时参数是固定的。
\[\begin {equation} L_{\mathrm{nsf}}=\sum_{\mathbf{x} \in \mathcal{X}_{i}}\left\|\mathbf{w}_{i}(\mathbf{x})-\mathbf{w}^{\mathrm{can}}\left(T_{i}(\mathbf{x})\right)\right\|_{1} \end {equation}\]$\mathcal{X}_i$ 是第 $i$ 帧 3D bbox内的采样点集合。
训练时上面两个 Loss function 的系数都是 1。
4 驱动 Animation
4.1 新视点合成 Image Synthesis
给定一个新的 pose,首先更新 SMPL pose参数 $S ^ \text{new}$,并且由此计算SMPL蒙皮权重 $\mathbf w_\text{s}$,新的neural blend weight field $\mathbf w^ \text{new}$ 定义为:
\[\begin {equation} \mathbf{w}^{\text {new }}\left(\mathbf{x}, \boldsymbol{\psi}^{\text {new }}\right)=\operatorname{norm}\left(F_{\Delta \mathbf{w}}\left(\mathbf{x}, \boldsymbol{\psi}^{\text {new }}\right)+\mathbf{w}^{\mathrm{s}}\left(\mathbf{x}, S^{\text {new }}\right)\right) \end {equation}\]基于 $\mathbf w ^\text{new}$ 和LBS模型,我们可以产生新的 deformation field 形变场 $T^\text{new}$。需要重新训练的是 latent code $\psi ^ \text{new}$,由下式优化:
\[\begin {equation} L_{\text {new }}=\sum_{\mathbf{x} \in \mathcal{X}^{\text {new }}}\left\|\mathbf{w}^{\text {new }}(\mathbf{x})-\mathbf{w}^{\text {can }}\left(T^{\text {new }}(\mathbf{x})\right)\right\|_{1} \end {equation}\]$\mathcal{X}^\text{new}$ 是新动作下 3D bbox内的采样点集合。注意 $\mathbf{w}^{\text {can }}$ 在训练新动作的人体模型时参数是固定的。
实际上不同动作的skinning field通过改变latent code同时训练。
4.2 3D表面重建 3D shape Generation
类似neural body,把bbox分成voxel,根据 density 值采用 marching cubes 算法提取出 mesh。
新 pose 使用公式(3)转换每个 vertex 位置,产生形变后的mesh。
实现细节
NeRF的 密度场F$\sigma$ 和颜色场 $F\mathbf c$ 和原论文中一样。这里仅仅使用单次采样,每条光线采 64 个点。
$F_{\Delta \mathbf{w}}$ 的结构和上面两个几乎一样,区别是最后一层输出 24 维,此外,对结果应用需要应用 $\text{exp}(·)$。

网络架构

实验结果



